More infinitely divisible noise addition
This a follow-up to my previous post about infinitely divisible noise addition. There, I outlined the privacy guarantee of the difference of two negative binomial random variables, called the generalized discrete Laplace (GDL) distribution.
My colleague Pasin Manurangsi and I expanded on this result in a new paper accepted to FORC ‘25: Infinitely Divisible Noise for Differential Privacy: Nearly Optimal Error in the High $\varepsilon$ Regime. Beyond formalizing the privacy proof of the GDL mechanism (and the proof of its $O(e^{-\epsilon})$ MSE), we came up with another even stranger infinitely divisible distribution for $\Delta$-summation called the multi-scale discrete Laplace (MSDLap) distribution.

For $X_1, \dots, X_\Delta \overset{iid}\sim \DLap(\epsilon)$, the $(\epsilon, \Delta)$-MSDLap distribution is defined as $Y \sim \sum_{i=1}^\Delta i\cdot X_i$. i.e. it is the sum of $\Delta$ different $\DLap$ random variables, each at different scales.
Informally, we can reason about the privacy of the mechanism as follows: for $\Delta$-summation, each user can submit a value in $\{0, 1, \dots, \Delta\}$. Obviously if the user submits 0 the sum is the same regardless of whether they contribute or not. If the user submits 1, we can privatize it (relative to its absence) by adding $\DLap(\epsilon)$ noise. Likewise if the user submits any $x \le \Delta$ it suffices to add $x \cdot \DLap(\epsilon)$ to privatize the presence/absence of that particular value. Since MSDLap adds noise for all possible values the user could submit, we achieve $\epsilon$-DP.
For utility, the MSE of the mechanism is
\[\begin{align*} \Var[Y] &= \sum_{i=1}^\Delta i^2 \Var[\DLap(\epsilon)]\\ &= \frac{1}{\cosh(\epsilon)-1} \sum_{i=1}^\Delta i^2 \\ &= \left(\frac{1}{\cosh(\epsilon)-1}\right) \frac{1}{6} \Delta (\Delta + 1) (2 \Delta + 1)\\ &= O(\Delta^3 e^{-\epsilon}). \end{align*}\]The PMF of MSDLap is “staircase” shaped, like the optimal mechanism from Geng and Viswanath ‘14, and it can achieve a much better MSE than the GDL mechanism we studied before. However, it still has a $O(\Delta^3)$ dependence on the sensitivity, which is not necessarily the best dependence. In fact, the staircase mechanism can be parameterized by a parameter ($r$), to achieve $O(\min(\Delta^3 e^{-\epsilon}, \Delta^2 e^{-2\epsilon/3}))$. We can generalize the MSDLap mechanism similarly.
$r$-parameterized MSDLap
Assume for simplicity $\epsilon > 2$. For $r \in \{1, \dots, \Delta\}$, our mechanism will add noise from $Y + Z$ where $Y \sim r \cdot (\epsilon - 1, \lfloor \Delta / r \rfloor)$-MSDLap, and $Z \sim \DLap(1/r)$. At a high level, $Y$ adds noise from a “scaled up” MSDLap, which fails to protect all inputs because there are holes in its support when $r > 1$. Informally, the proof proceeds by decomposing an arbitrary user input $\xi = r\cdot i^* + j^*$, where \(i^* = \lfloor \xi / r \rfloor\) and \(j^* = \xi - r \cdot i^*\).
We can think of \(r \cdot i^*\) as the portion of the input protected by the MSDLap noise, and \(j^*\) (which has sensitivity $r$) as the “remainder” of the input which is protected by the regular $\DLap$ noise. From composition, the MSDLap noise protects \(r\cdot i^*\) with $\epsilon - 1$-DP and the $\DLap$ noise protects \(j^*\) with 1-DP, so the whole mechanism is $\epsilon$-DP.
For accuracy, note that that
\[\begin{align*} \Var[Y + Z] &= \Var[Y] + \Var[Z]\\ &= O(r^2 \frac{\Delta^3}{r^3} e^{-\epsilon}) + O(r^2)\\ &= O(r^2 + \Delta^3 e^{-\epsilon} /r) \end{align*}\]Setting \(r = \lceil \Delta e^{-\epsilon/3} \rceil\) yields an MSE of \(O(\Delta^2 e^{-2\epsilon /3})\) as desired. Below we plot the best MSE we can get from MSDLap along with the GDL mechanism.
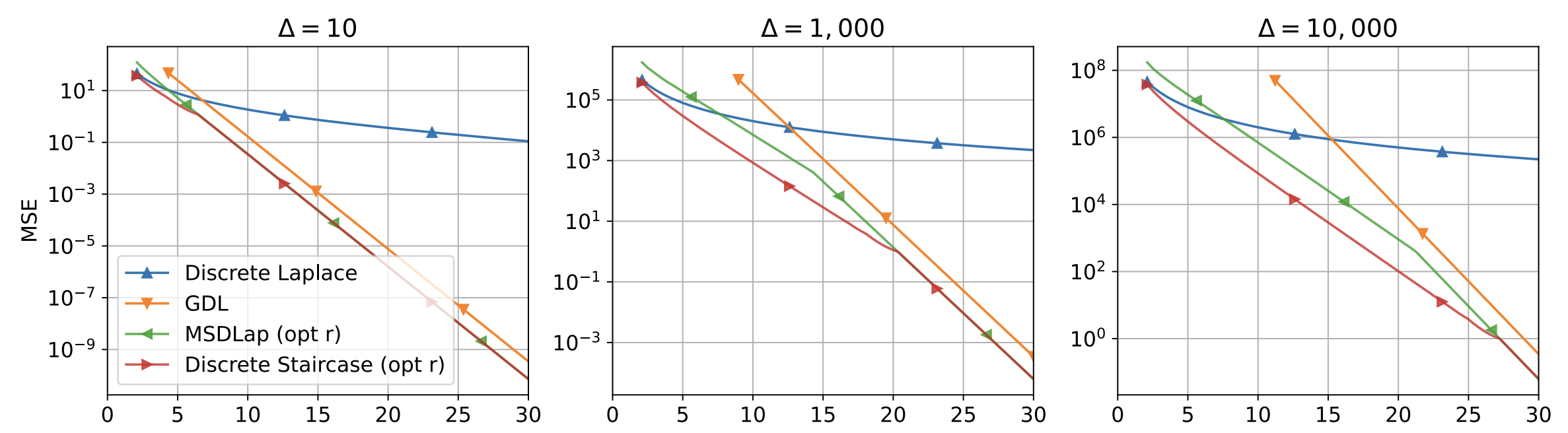
We show more results in the paper, including:
- Actual proofs :)
- Showing a technique to transform a discrete mechanism to a continuous one, by “filling the holes” in the support of a discrete distributions with a small amount of continuous noise, in the same way we did with the $r$-parameterized MSDLap. In this case though, the “remainder” is continuous!
- Providing an algorithm to efficiently sample from the MSDLap distribution, which involves sampling many negative binomial random variables.
- Improving the IKOS multi-message shuffle protocol of Balle et. al and Ghazi et al. for real summation to give $O(\Delta^2 e^{-2 \epsilon /3})$ MSE.