The staircase mechanism in differential privacy was introduced by Geng & Viswanath 2012. In a previous post we benchmarked the GDL mechanism against the staircase, but I couldn’t find an analytical formula for the variance of the discrete variant. In this post I’ll try to get a closed form expression.

Let’s start with some background. The staircase mechanism is a dataset-independent noise addition mechanism, similar to the (discrete) laplace mechanism. However, it outperforms the Laplace mechanism under a bunch of utility metrics, especially when $\epsilon$ is large.

The PMF for the univariate discrete staircase distribution is defined as:

\[P_r(i) = \begin{cases} a(r) & 0 \le i < r \\ a(r)e^{-\epsilon} & r \le i < \Delta\\ e^{-k \epsilon}P_r(i - k\Delta) & k \Delta \le i < (k + 1) \Delta \text{ for } k \in \mathbb{N}\\ P_r(-i) & i < 0 \end{cases}\]

where

\[a(r) = \frac{1-b}{2r + 2b(\Delta - r) - (1-b)}\]

for $b = e^{-\epsilon}$.

Here it is plotted out, for $r=3$ and $\Delta=5$ (copied from the paper).

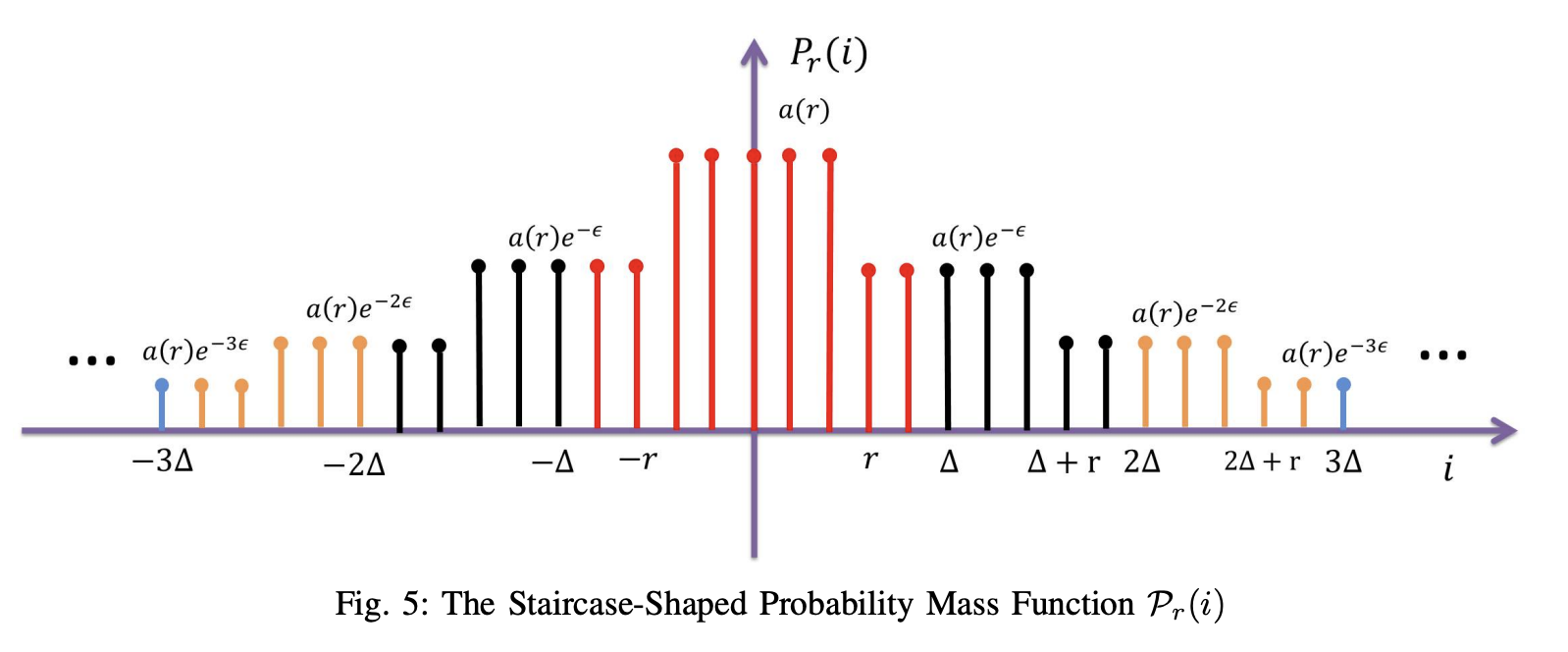
Discrete Staircase

Let’s compute the variance. Let $X$ be distributed according to the discrete staircase distribution with parameters $r$, $\Delta$, and $\epsilon$. To help with the computations, note that the width of the central “stair” is $2r-1$ and the width of all other stairs are $\Delta$.

\[\begin{align*} E[X^2] &= \sum_{x=-\infty}^\infty P_r(i) x^2\\ &= \sum_{x=-r+1}^{r-1} x^2 a(r) + 2\sum_{k=1}^\infty \sum_{i=1}^\Delta ((k-1) \Delta + r + i - 1)^2 P_r(k \Delta - r + i)\\ &= \frac{1}{3}r(r-1)(2r-1) a(r) + 2\sum_{k=1}^\infty \sum_{i=1}^\Delta ((k-1) \Delta + r + i - 1)^2 a(r)e^{-k\epsilon}\\ \end{align*}\]

Woah wait a sec this is getting kind of hairy. Let’s just do $r=1$ which is the parameterization in our previous post (which minimizes variance for large $\epsilon$), so

\[\begin{align*} a(1) &= \frac{1-b}{2 + 2b(\Delta - 1) - (1-b)}\\ &= \frac{e^\epsilon - 1}{2\Delta + e^\epsilon - 1} \end{align*}\]

The variance of the central column is 0 since it’s just a single point. Therefore, with the magic of Wolfram Alpha:

\[\begin{align*} E[X^2] &= \frac{\Delta (8 \Delta^2 e^\epsilon + 2 \Delta^2 e^{2\epsilon} + 2\Delta^2 + 3\Delta e^{2\epsilon} - 3\Delta - 2e^\epsilon + e^{2 \epsilon} + 1)}{3(e^\epsilon -1)^2 (2 \Delta + e^\epsilon -1)} \end{align*}\]

This is pretty gnarly. Let’s plot it to make sure it matches the numeric estimation:

Variance of the discrete staircase

Nice, looks good! If I ever need the general form with $r > 1$. I will update this post with the full formula. Right now it is too nasty for me to want to write down.

For now let’s just conclude with some asymptotics. In the previous post I mentioned that this is $O(e^{-\epsilon})$ variance. Taking the limit shows that indeed:

\[\lim_{\epsilon->\infty} E[X^2] e^{\epsilon} = \frac{1}{3}\Delta (1 + \Delta) (1 + 2\Delta)\]

So the variance is $\Theta(\Delta^3 e^{-\epsilon})$. From the plots it appears we approach this limiting behavior quickly for small $\Delta$. Let’s see this more clearly by plotting the limiting behavior:

Asymptotic variance of the discrete staircase

It is fascinating to see a cubic relationship with $\Delta$!